Lets start with something simple and fun.
The Fibonacci numbers are Nature's numbering system. They appear everywhere in Nature, from the leaf arrangement in plants, to the pattern of the florets of a flower, the bracts of a pine-cone, or the scales of a pineapple. The Fibonacci numbers are therefore applicable to the growth of every living thing, including a single cell, a grain of wheat, a hive of bees, and even all of mankind.
In mathematics, the Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers in the following integer sequence:
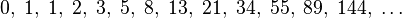
By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two.
The next number is found by adding up the two numbers before it.
The next number is found by adding up the two numbers before it.
- The 2 is found by adding the two numbers before it (1+1)
- Similarly, the 3 is found by adding the two numbers before it (1+2),
- And the 5 is (2+3),
- and so on!
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
with seed values
Here is a simplest Java Program to generate Fibonacci Series.
Here is a simplest Java Program to generate Fibonacci Series.
public static int dnrFibonacciSeries(int n){
if(n == 1 || n == 2){
return 1;
}
int fiboTemp1=1, fiboTemp2=1, fibonacci=1;
for(int i= 3; i<= n; i++){
fibonacci = fiboTemp1 + fiboTemp2; //Fibonacci number is sum of previous two Fibonacci number
fiboTemp1 = fiboTemp2;
fiboTemp2 = fibonacci;
}
return fibonacci; //Fibonacci number
}
Here is it's recursive version.
public static int dnrFibonacciRecursive(int n)
{
if ( n == 0 )
return 0;
else if ( n == 1 )
return 1;
else
return ( dnrFibonacciRecursive(n-1) + dnrFibonacciRecursive(n-2) );
}
Here's a TED talk that inspires interest in such sequence
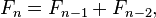
No comments:
Post a Comment