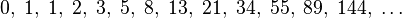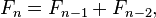Factorial (n!) - Symmetry in nature II

Factorials are very simple things. They're just products, indicated by an exclamation mark. For instance, "four factorial" is written as "4!" and means 1×2×3×4 = 24

For n=0,

0! = 1

The factorial operation is encountered in many areas of mathematics, notably in combinatorics, algebra, and mathematical analysis. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence (i.e., permutations of the set of objects). This fact was known at least as early as the 12th century, to Indian scholars.

Factorial definition formula

Examples:

1! = 1

2! = 1×2 = 2

3! = 1×2×3 = 6

4! = 1×2×3×4 = 24

5! = 1×2×3×4×5 = 120

Recursive factorial formula

n! = n×(n-1)!

Example:

5! = 5×(5-1)! = 5×4! = 5×24 = 120

Applications : 

Permutation Formula A formula for the number of possible permutations of k objects from a set of n. This is usually written nPr = n(n - 1)(n - 2) ... (n - r + 1) =n!(n - r)! Example : How many ways 4 students from a group of 15 be lined up for a photograph ? Answer :  There are 15P4     possible permutations of 4 students from a group of 15.                         15P4  = 15! / 11! = 15 * 14 * 13 * 12 = 32760 different lineups.  Combination Formula A formula for the number of possible combinations of r objects from a set of n objects. This is written in any of the ways shown below nCr =n!=n(n - 1)(n - 2) ... to r factors.(r!)(n - r)!r! Note: nCn = 1 and nC0 = 1. nCr = nC(n - r)

 Example : How many different committees of 4 students can be chosen from a group of 15?

 Answer : There are  possible combinations of 4 students from a set of 15

 = 15! / 4!11! = (15 * 14 *3) / (4 * 3 *2  *1 ) = 1365 

  public static long dnrFactorial(int n)  
       {  
         int c;    
         long result = 1;  
         for( c = 1 ; c <= n ; c++ )  
              result = result*c;  
              return ( result );  
       }  

Recursive Function : 

  public static long dnrFactorialRecursive(int n)  
       {  
            if (n == 0)  
                 return 1;  
            else  
                 return n * dnrFactorialRecursive(n-1);  
       }  

The Fibonacci series : Symmetry in nature I

Lets start with something simple and fun.

The Fibonacci numbers are Nature's numbering system. They appear everywhere in Nature, from the leaf arrangement in plants, to the pattern of the florets of a flower, the bracts of a pine-cone, or the scales of a pineapple. The Fibonacci numbers are therefore applicable to the growth of every living thing, including a single cell, a grain of wheat, a hive of bees, and even all of mankind.

In mathematics, the Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers in the following integer sequence:  

By definition, the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the previous two.
 The next number is found by adding up the two numbers before it.

• The 2 is found by adding the two numbers before it (1+1)
• Similarly, the 3 is found by adding the two numbers before it (1+2),
• And the 5 is (2+3),
• and so on!

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation

with seed values
Here is a simplest Java Program to generate Fibonacci Series.

       public static int dnrFibonacciSeries(int n){  
          if(n == 1 || n == 2){  
            return 1;  
          }  
          int fiboTemp1=1, fiboTemp2=1, fibonacci=1;  
          for(int i= 3; i<= n; i++){  
            fibonacci = fiboTemp1 + fiboTemp2; //Fibonacci number is sum of previous two Fibonacci number  
            fiboTemp1 = fiboTemp2;  
            fiboTemp2 = fibonacci;  
          }  
          return fibonacci; //Fibonacci number  
        }    

Here is it's recursive version.

 public static int dnrFibonacciRecursive(int n)  
       {  
        if ( n == 0 )  
          return 0;  
        else if ( n == 1 )  
          return 1;  
        else  
          return ( dnrFibonacciRecursive(n-1) + dnrFibonacciRecursive(n-2) );  
       }   

Here's a TED talk that inspires interest in such sequence